Find minimum cost to reach the last cell of a matrix from its first cell
Given an M × N matrix of integers where each cell has a cost associated with it, find the minimum cost to reach the last cell (M-1, N-1) of the matrix from its first cell (0, 0). We can only move one unit right or one unit down from any cell, i.e., from cell (i, j), we can move to (i, j+1) or (i+1, j).
For example,

The highlighted path shows the minimum cost path having a cost of 36.
The idea is to use recursion. The problem has optimal substructure. That means the problem can be broken down into smaller, simple “subproblems”, which can further be divided into yet simpler, smaller subproblems until the solution becomes trivial. We can recursively define the problem as:
cost to reach cell (m, n-1))
Following is the C++, Java, and Python implementation of the idea:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
#include <iostream> #include <climits> #include <vector> using namespace std; // Naive recursive function to find the minimum cost to reach // cell (m, n) from cell (0, 0) int findMinCost(vector<vector<int>> const &cost, int m, int n) { // base case if (n == 0 || m == 0) { return INT_MAX; } // if we are in the first cell (0, 0) if (m == 1 && n == 1) { return cost[0][0]; } // include the current cell's cost in the path and recur to find the minimum // of the path from the adjacent left cell and adjacent top cell. return min (findMinCost(cost, m - 1, n), findMinCost(cost, m, n - 1)) + cost[m - 1][n - 1]; } int findMinCost(vector<vector<int>> const &cost) { // base case if (cost.size() == 0) { return 0; } // `M × N` matrix int M = cost.size(); int N = cost[0].size(); return findMinCost(cost, M, N); } int main() { vector<vector<int>> cost = { { 4, 7, 8, 6, 4 }, { 6, 7, 3, 9, 2 }, { 3, 8, 1, 2, 4 }, { 7, 1, 7, 3, 7 }, { 2, 9, 8, 9, 3 } }; cout << "The minimum cost is " << findMinCost(cost); return 0; } |
Output:
The minimum cost is 36
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
class Main { // Naive recursive function to find the minimum cost to reach // cell (m, n) from cell (0, 0) public static int findMinCost(int[][] cost, int m, int n) { // base case if (n == 0 || m == 0) { return Integer.MAX_VALUE; } // if we are in the first cell (0, 0) if (m == 1 && n == 1) { return cost[0][0]; } // include the current cell's cost in the path and recur to find the minimum // of the path from the adjacent left cell and adjacent top cell. return Integer.min(findMinCost(cost, m - 1, n), findMinCost(cost, m, n - 1)) + cost[m - 1][n - 1]; } public static int findMinCost(int[][] cost) { // base case if (cost == null || cost.length == 0) { return 0; } return findMinCost(cost, cost.length, cost[0].length); } public static void main(String[] args) { int[][] cost = { { 4, 7, 8, 6, 4 }, { 6, 7, 3, 9, 2 }, { 3, 8, 1, 2, 4 }, { 7, 1, 7, 3, 7 }, { 2, 9, 8, 9, 3 } }; System.out.println("The minimum cost is " + findMinCost(cost)); } } |
Output:
The minimum cost is 36
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
import sys # Naive recursive function to find the minimum cost to reach # cell (m, n) from cell (0, 0) def findMinCost(cost, m=None, n=None): # initialize m and n if not m and not n: m, n = len(cost), len(cost[0]) # base case if not cost or not len(cost): return 0 # base case if n == 0 or m == 0: return sys.maxsize # if we are in the first cell (0, 0) if m == 1 and n == 1: return cost[0][0] # include the current cell's cost in the path and recur to find the minimum # of the path from the adjacent left cell and adjacent top cell. return min(findMinCost(cost, m - 1, n), findMinCost(cost, m, n - 1))\ + cost[m - 1][n - 1] if __name__ == '__main__': cost = [ [4, 7, 8, 6, 4], [6, 7, 3, 9, 2], [3, 8, 1, 2, 4], [7, 1, 7, 3, 7], [2, 9, 8, 9, 3] ] print('The minimum cost is', findMinCost(cost)) |
Output:
The minimum cost is 36
The time complexity of the proposed solution is exponential as we are doing a lot of redundant work. For example, consider the recursion tree for a 5 × 5 matrix.
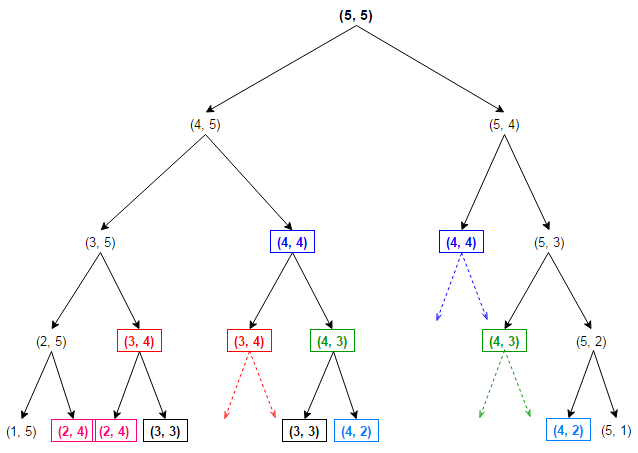
As we can see, the same subproblems (highlighted in the same color) are getting computed repeatedly. As the recursion grows deeper, more and more of this type of unnecessary repetition occurs. We know that problems having optimal substructure and overlapping subproblems can be solved by dynamic programming, in which subproblem solutions are memoized rather than computed repeatedly. Each time we calculate the minimum cost of reaching any cell (i, j), we save it. If we are ever asked to compute it again, give the saved answer and do not recompute it.
The following bottom-up approach computes, for each 0 <= i < M and 0 <= j < N, the minimum costs of reaching cell (i, j) from cell (0, 0), using the costs of smaller values i and j already computed. It has the same asymptotic runtime as Memoization but no recursion overhead.
Following is the C++, Java, and Python implementation of the idea:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
#include <iostream> #include <string> #include <vector> #include <algorithm> using namespace std; // Iterative function to find the minimum cost to traverse from the // first cell to the last cell of a matrix int findMinCost(vector<vector<int>> const &cost) { // base case if (cost.size() == 0) { return 0; } // `M × N` matrix int M = cost.size(); int N = cost[0].size(); // `T[i][j]` maintains the minimum cost to reach cell (i, j) from cell (0, 0) int T[M][N]; // fill the matrix in a bottom-up manner for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { T[i][j] = cost[i][j]; // fill the first row (there is only one way to reach any cell in // the first row from its adjacent left cell) if (i == 0 && j > 0) { T[0][j] += T[0][j - 1]; } // fill the first column (there is only one way to reach any cell // in the first column from its adjacent top cell) else if (j == 0 && i > 0) { T[i][0] += T[i - 1][0]; } // fill the rest with the matrix (there are two ways to reach any cell // in the rest of the matrix, from its adjacent left // cell or adjacent top cell) else if (i > 0 && j > 0) { T[i][j] += min(T[i - 1][j], T[i][j - 1]); } } } // last cell of `T[][]` stores the minimum cost to reach destination cell // (M-1, N-1) from source cell (0, 0) return T[M - 1][N - 1]; } int main() { vector<vector<int>> cost = { { 4, 7, 8, 6, 4 }, { 6, 7, 3, 9, 2 }, { 3, 8, 1, 2, 4 }, { 7, 1, 7, 3, 7 }, { 2, 9, 8, 9, 3 } }; cout << "The minimum cost is " << findMinCost(cost); return 0; } |
Output:
The minimum cost is 36
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
class Main { // Iterative function to find the minimum cost to traverse // from the first cell to the last cell of a matrix public static int findMinCost(int[][] cost) { // base case if (cost == null || cost.length == 0) { return 0; } // `M × N` matrix int M = cost.length; int N = cost[0].length; // `T[i][j]` maintains the minimum cost to reach cell (i, j) // from cell (0, 0) int[][] T = new int[M][N]; // fill the matrix in a bottom-up manner for (int i = 0; i < M; i++) { for (int j = 0; j < N; j++) { T[i][j] = cost[i][j]; // fill the first row (there is only one way to reach any cell // in the first row from its adjacent left cell) if (i == 0 && j > 0) { T[0][j] += T[0][j - 1]; } // fill the first column (there is only one way to reach any cell // in the first column from its adjacent top cell) else if (j == 0 && i > 0) { T[i][0] += T[i - 1][0]; } // fill the rest with the matrix (there are two ways to reach any // cell in the rest of the matrix, from its adjacent // left cell or adjacent top cell) else if (i > 0 && j > 0) { T[i][j] += Integer.min(T[i - 1][j], T[i][j - 1]); } } } // last cell of `T[][]` stores the minimum cost to reach destination cell // (M-1, N-1) from source cell (0, 0) return T[M - 1][N - 1]; } public static void main(String[] args) { int[][] cost = { { 4, 7, 8, 6, 4 }, { 6, 7, 3, 9, 2 }, { 3, 8, 1, 2, 4 }, { 7, 1, 7, 3, 7 }, { 2, 9, 8, 9, 3 } }; System.out.print("The minimum cost is " + findMinCost(cost)); } } |
Output:
The minimum cost is 36
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# Iterative function to find the minimum cost to traverse from the # first cell to the last cell of a matrix def findMinCost(cost): # `M × N` matrix (M, N) = (len(cost), len(cost[0])) # `T[i][j]` maintains the minimum cost to reach cell (i, j) from cell (0, 0) T = [[0 for x in range(N)] for y in range(M)] # fill the matrix in a bottom-up manner for i in range(M): for j in range(N): T[i][j] = cost[i][j] # fill the first row (there is only one way to reach any cell in the # first row from its adjacent left cell) if i == 0 and j > 0: T[0][j] += T[0][j - 1] # fill the first column (there is only one way to reach any cell in # the first column from its adjacent top cell) elif j == 0 and i > 0: T[i][0] += T[i - 1][0] # fill the rest with the matrix (there are two ways to reach any # cell in the rest of the matrix, from its adjacent # left cell or adjacent top cell) elif i > 0 and j > 0: T[i][j] += min(T[i - 1][j], T[i][j - 1]) # last cell of `T[][]` stores the minimum cost to reach destination cell # (M-1, N-1) from source cell (0, 0) return T[M - 1][N - 1] if __name__ == '__main__': cost = [ [4, 7, 8, 6, 4], [6, 7, 3, 9, 2], [3, 8, 1, 2, 4], [7, 1, 7, 3, 7], [2, 9, 8, 9, 3] ] print("The minimum cost is", findMinCost(cost)) |
Output:
The minimum cost is 36
The time complexity of the proposed solution is O(M × N) for an M × N matrix. The auxiliary space required by the program is O(M × N).
Exercise: Extend the solution to consider diagonal moves as well.
Calculate the minimum cost to reach the destination city from the source city
Count the number of paths in a matrix with a given cost to reach the destination cell
Count all paths in a matrix from the first cell to the last cell
Thanks for reading.
To share your code in the comments, please use our online compiler that supports C, C++, Java, Python, JavaScript, C#, PHP, and many more popular programming languages.
Like us? Refer us to your friends and support our growth. Happy coding :)