给定一棵二叉树,求其中最大独立集 (MIS) 的大小。
独立集是二叉树中的一组节点,其中没有两个是相邻的,即没有边连接任何两个。独立集的大小是它包含的节点总数。最大独立集问题是为给定的二叉树找到最大可能大小的独立集。
例如,以下二叉树的最大独立集(MIS)为 [1, 4, 6, 7, 8].
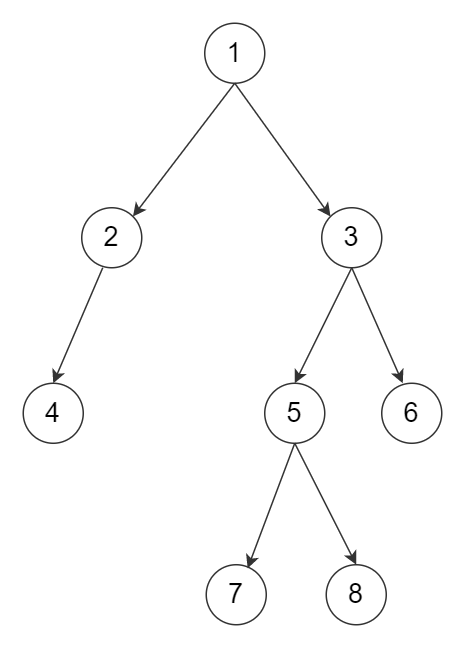
从上面的例子可以看出,如果一个节点被认为是 MIS 的一部分,那么它的左右子节点就不能成为 MIS 的一部分。但是,它的子孙可以成为 MIS 的一部分。
思路是遍历二叉树,对于二叉树中的每个节点,有两种可能的情况:
- 从最大独立集中排除当前节点并处理其子节点。
- 将当前节点包含在最大独立集中并处理其孙子节点。
因此,通过包含或排除当前节点来返回可能的最大节点数。该算法可以在 C++、Java 和 Python 中递 归地实现如下:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
#include <iostream> using namespace std; // 存储二叉树节点的数据结构 struct Node { int data; Node *left, *right; Node(int data) { this->data = data; this->left = this->right = nullptr; } }; // 递归的函数求最大独立集的大小 // 对于二叉树 int findMISSize(Node* root) { // 基本情况:空树 if (root == nullptr) { return 0; } // 情况一:从最大独立集中排除当前节点, // 为其左右孩子递归 int excl = findMISSize(root->left) + findMISSize(root->right); // 情况2:将当前节点包含在最大独立集中并且 // 为它的子孙重复 int incl = 1; if (root->left) { incl += findMISSize(root->left->left) + findMISSize(root->left->right); } if (root->right) { incl += findMISSize(root->right->left) + findMISSize(root->right->right); } // 返回可能的最大节点数 // 包含或排除当前节点 return max(excl, incl); } int main() { Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->right->left = new Node(5); root->right->right = new Node(6); root->right->left->left = new Node(7); root->right->left->right = new Node(8); cout << "The size of a maximum independent set is " << findMISSize(root); return 0; } |
输出:
The size of a maximum independent set is 5
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 |
// 存储二叉树节点的数据结构 class Node { int data; Node left, right; Node(int data) { this.data = data; this.left = this.right = null; } } class Main { // 递归的函数求最大独立集的大小 // 对于二叉树 public static int findMISSize(Node root) { // 基本情况:空树 if (root == null) { return 0; } // 情况一:从最大独立集中排除当前节点, // 为其左右孩子递归 int excl = findMISSize(root.left) + findMISSize(root.right); // 情况2:将当前节点包含在最大独立集中并且 // 为它的子孙重复 int incl = 1; if (root.left != null) { incl += findMISSize(root.left.left) + findMISSize(root.left.right); } if (root.right != null) { incl += findMISSize(root.right.left) + findMISSize(root.right.right); } // 返回可能的最大节点数 // 包含或排除当前节点 return Integer.max(excl, incl); } public static void main(String[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.right.left = new Node(5); root.right.right = new Node(6); root.right.left.left = new Node(7); root.right.left.right = new Node(8); System.out.println("The size of a maximum independent set is " + findMISSize(root)); } } |
输出:
The size of a maximum independent set is 5
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
# 存储二叉树节点的数据结构 class Node: def __init__(self, data, left=None, right=None): self.data = data self.left = left self.right = right #递归的函数求最大独立集的大小 # 二叉树的 def findMISSize(root): # 基础案例:空树 if root is None: return 0 # 案例1:从最大独立集中排除当前节点, # 为其左右孩子重复 excl = findMISSize(root.left) + findMISSize(root.right) # 案例2:将当前节点包含在最大独立集中,并且 # 为其孙辈重现 incl = 1 if root.left: incl += findMISSize(root.left.left) + findMISSize(root.left.right) if root.right: incl += findMISSize(root.right.left) + findMISSize(root.right.right) # 返回可能的最大节点数 # 包括或不包括当前节点 return max(excl, incl) if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.right.left = Node(5) root.right.right = Node(6) root.right.left.left = Node(7) root.right.left.right = Node(8) print('The size of a maximum independent set is', findMISSize(root)) |
输出:
The size of a maximum independent set is 5
上述解决方案的时间复杂度是指数级的,并且需要额外的递归空间(调用堆栈)。
可以看出问题有 最优子结构 因为它可以分解为更小的子问题,这些子问题可以进一步分解为更小的子问题,依此类推。问题也表现在 重叠子问题,所以我们最终将一遍又一遍地解决相同的子问题。
我们知道具有最优子结构和重叠子问题的问题可以通过动态规划来解决,其中子问题的解决方案是 备忘录化以避免重新计算相同的子问题。动态编程解决方案可以用 C++、Java 和 Python 实现如下:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
#include <iostream> #include <unordered_map> using namespace std; // 存储二叉树节点的数据结构 struct Node { int data; Node *left, *right; Node(int data) { this->data = data; this->left = this->right = nullptr; } }; // 递归的函数求最大独立集的大小 // 对于二叉树 int findMISSize(Node* root, unordered_map<Node*, int> map) { // 基本情况:空树 if (root == nullptr) { return 0; } if (map.find(root) != map.end()) { return map[root]; } // 情况一:从最大独立集中排除当前节点, // 为其左右孩子递归 int excl = findMISSize(root->left, map) + findMISSize(root->right, map); // 情况2:将当前节点包含在最大独立集中并且 // 为它的子孙重复 int incl = 1; if (root->left) { incl += findMISSize(root->left->left, map) + findMISSize(root->left->right, map); } if (root->right) { incl += findMISSize(root->right->left, map) + findMISSize(root->right->right, map); } // 保存并返回可能的最大节点数 // 包含或排除当前节点 map[root] = max(excl, incl); return map[root]; } int main() { Node* root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->right->left = new Node(5); root->right->right = new Node(6); root->right->left->left = new Node(7); root->right->left->right = new Node(8); unordered_map<Node*, int> map; cout << "The size of a maximum independent set is " << findMISSize(root, map); return 0; } |
输出:
The size of a maximum independent set is 5
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
import java.util.HashMap; import java.util.Map; // 存储二叉树节点的数据结构 class Node { int data; Node left, right; Node(int data) { this.data = data; this.left = this.right = null; } } class Main { // 递归的函数求最大独立集的大小 // 对于二叉树 public static int findMIS(Node root, Map<Node, Integer> map) { // 基本情况:空树 if (root == null) { return 0; } if (map.get(root) != null) { return map.get(root); } // 情况一:从最大独立集中排除当前节点, // 为其左右孩子递归 int excl = findMIS(root.left, map) + findMIS(root.right, map); // 情况2:将当前节点包含在最大独立集中并且 // 为它的子孙重复 int incl = 1; if (root.left != null) { incl += findMIS(root.left.left, map) + findMIS(root.left.right, map); } if (root.right != null) { incl += findMIS(root.right.left, map) + findMIS(root.right.right, map); } // 保存并返回可能的最大节点数 // 包含或排除当前节点 map.put(root, Integer.max(excl, incl)); return map.get(root); } public static void main(String[] args) { Node root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.right.left = new Node(5); root.right.right = new Node(6); root.right.left.left = new Node(7); root.right.left.right = new Node(8); Map<Node, Integer> map = new HashMap<>(); System.out.println("The size of a maximum independent set is " + findMIS(root, map)); } } |
输出:
The size of a maximum independent set is 5
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# 存储二叉树节点的数据结构 class Node: def __init__(self, data, left=None, right=None): self.data = data self.left = left self.right = right #递归的函数求最大独立集的大小 # 二叉树的 def findMIS(root, d): # 基础案例:空树 if root is None: return 0 if root in d: return d[root] # 案例1:从最大独立集中排除当前节点, # 为其左右孩子重复 excl = findMIS(root.left, d) + findMIS(root.right, d) # 案例2:将当前节点包含在最大独立集中,并且 # 为其孙辈重现 incl = 1 if root.left: incl += findMIS(root.left.left, d) + findMIS(root.left.right, d) if root.right: incl += findMIS(root.right.left, d) + findMIS(root.right.right, d) # 保存并返回可能的最大节点数 # 包括或不包括当前节点 d[root] = max(excl, incl) return d[root] if __name__ == '__main__': root = Node(1) root.left = Node(2) root.right = Node(3) root.left.left = Node(4) root.right.left = Node(5) root.right.right = Node(6) root.right.left.left = Node(7) root.right.left.right = Node(8) d = {} print('The size of a maximum independent set is', findMIS(root, d)) |
输出:
The size of a maximum independent set is 5
上述解决方案的时间复杂度为 O(n) 并要求 O(n) 额外的空间,在哪里 n 是二叉树中节点的总数。