Algoritmo de compresión de codificación de Huffman
La codificación Huffman (también conocida como Codificación Huffman) es un algoritmo para realizar la compresión de datos y forma la idea básica detrás de la compresión de archivos. Esta publicación habla sobre la codificación de longitud fija y de longitud variable, los códigos decodificables únicos, las reglas de prefijo y la construcción del árbol de Huffman.
Visión general
Ya sabemos que todo personaje son secuencias de 0's y 1's y se almacena usando 8 bits. Esto se conoce como "codificación de longitud fija", ya que cada carácter usa la misma cantidad de almacenamiento de bits fijos.
Dado un texto, ¿cómo reducir la cantidad de espacio requerido para almacenar un carácter?
La idea es utilizar "codificación de longitud variable". Podemos aprovechar el hecho de que algunos caracteres aparecen con más frecuencia que otros en un texto (consulte este) para diseñar un algoritmo que pueda representar el mismo fragmento de texto utilizando un número menor de bits. En la codificación de longitud variable, asignamos un número variable de bits a los caracteres según su frecuencia en el texto dado. Entonces, algunos caracteres podrían terminar tomando un solo bit, y algunos podrían terminar tomando dos bits, algunos podrían codificarse usando tres bits, y así sucesivamente. El problema con la codificación de longitud variable radica en su decodificación.
Dada una secuencia de bits, ¿cómo decodificarla de forma única?
Consideremos la string aabacdab. Tiene 8 contiene caracteres y usa almacenamiento de 64 bits (usando codificación de longitud fija). Si anotamos, la frecuencia de caracteres a, b, c y d son 4, 2, 1, 1, respectivamente. Tratemos de representar aabacdab usando un número menor de bits usando el hecho de que a ocurre con más frecuencia que b, y b ocurre con más frecuencia que c y d. Comenzamos asignando aleatoriamente un código de un solo bit 0 a a, código de 2 bits 11 a by código de 3 bits 100 y 011 a personajes c y d, respectivamente.
b 11
c 100
d 011
Entonces, la string aabacdab será codificado para 00110100011011 (0|0|11|0|100|011|0|11) utilizando los códigos anteriores. Pero el verdadero problema radica en la decodificación. Si tratamos de decodificar la string 00110100011011, conducirá a la ambigüedad, ya que se puede decodificar,
0|0|11|0|100|0|11|011 aabacabd
0|011|0|100|0|11|0|11 adacabab
…
and so on
Para evitar ambigüedades en la decodificación, nos aseguraremos de que nuestra codificación satisfaga la "regla del prefijo", lo que dará como resultado "códigos decodificables de forma única". La regla del prefijo establece que ningún código es un prefijo de otro código. Por código, nos referimos a los bits utilizados para un carácter en particular. En el ejemplo anterior, 0 es el prefijo de 011, lo que viola la regla del prefijo. Si nuestros códigos satisfacen la regla del prefijo, la decodificación no será ambigua (y viceversa).
Consideremos de nuevo el ejemplo anterior. Esta vez asignamos códigos que cumplen la regla del prefijo a los caracteres 'a', 'b', 'c', y 'd'.
b 10
c 110
d 111
Usando los códigos anteriores, la string aabacdab será codificado para 00100110111010 (0|0|10|0|110|111|0|10). Ahora podemos decodificar de forma única 00100110111010 volver a nuestra string original aabacdab.
Ahora que tenemos claro la codificación de longitud variable y la regla de prefijo, hablemos de la codificación Huffman.
Codificación de Huffman
La técnica funciona creando un árbol binario de nodos Un nodo puede ser un nodo hoja o un nodo interno. Inicialmente, todos los nodos son nodos hoja, que contienen el carácter en sí, el peso (frecuencia de aparición) del carácter. Los nodos internos contienen peso de carácter y enlaces a dos nodos secundarios. Como convención común, un poco 0 representa seguir al hijo izquierdo, y un poco 1 representa seguir al hijo correcto. Un árbol terminado tiene n nudos de hojas y n-1 nodos internos. Se recomienda que Huffman Tree descarte los caracteres no utilizados en el texto para producir las longitudes de código más óptimas.
Usaremos un cola de prioridad para construir Huffman Tree, donde el nodo con la frecuencia más baja tiene la prioridad más alta. Los siguientes son los pasos completos:
1. Cree un nodo de hoja para cada personaje y agréguelo a la cola de prioridad.
2. Mientras haya más de un nodo en la queue:
- Quite los dos nodos de la prioridad más alta (la frecuencia más baja) de la queue.
- Cree un nuevo nodo interno con estos dos nodos como hijos y una frecuencia igual a la suma de las frecuencias de ambos nodos.
- Agregue el nuevo nodo a la cola de prioridad.
3. El nodo restante es el nodo raíz y el árbol está completo.
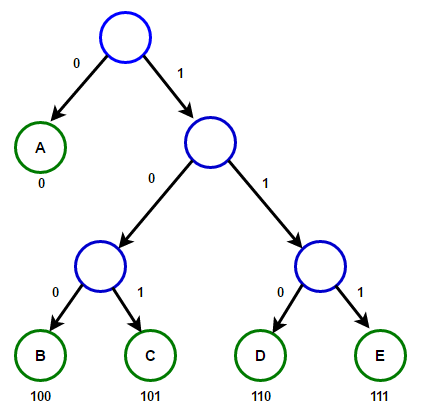
Considere un texto que consta de sólo 'A', 'B', 'C', 'D', y 'E' caracteres y sus frecuencias son 15, 7, 6, 6, 5, respectivamente. Las siguientes figuras ilustran los pasos seguidos por el algoritmo:





La ruta desde la raíz hasta cualquier nodo hoja almacena el código de prefijo óptimo (también llamado código Huffman) correspondiente al carácter asociado con ese nodo hoja.
Implementación
A continuación se muestra la implementación en C++, Java y Python del algoritmo de compresión de codificación de Huffman:
C++
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 |
#include <iostream> #include <string> #include <queue> #include <unordered_map> using namespace std; #define EMPTY_STRING "" // Un nodo de árbol struct Node { char ch; int freq; Node *left, *right; }; // Función para asignar un nuevo nodo de árbol Node* getNode(char ch, int freq, Node* left, Node* right) { Node* node = new Node(); node->ch = ch; node->freq = freq; node->left = left; node->right = right; return node; } // Objeto de comparación que se usará para ordenar el heap struct comp { bool operator()(const Node* l, const Node* r) const { // el elemento de mayor prioridad tiene la menor frecuencia return l->freq > r->freq; } }; // Función de utilidad para verificar si Huffman Tree contiene solo un solo nodo bool isLeaf(Node* root) { return root->left == nullptr && root->right == nullptr; } // Atraviesa el árbol de Huffman y almacena los códigos de Huffman en un mapa. void encode(Node* root, string str, unordered_map<char, string> &huffmanCode) { if (root == nullptr) { return; } // encontrado un nodo hoja if (isLeaf(root)) { huffmanCode[root->ch] = (str != EMPTY_STRING) ? str : "1"; } encode(root->left, str + "0", huffmanCode); encode(root->right, str + "1", huffmanCode); } // Atraviesa el árbol de Huffman y decodifica la string codificada void decode(Node* root, int &index, string str) { if (root == nullptr) { return; } // encontrado un nodo hoja if (isLeaf(root)) { cout << root->ch; return; } index++; if (str[index] == '0') { decode(root->left, index, str); } else { decode(root->right, index, str); } } // Construye Huffman Tree y decodifica el texto de entrada dado void buildHuffmanTree(string text) { // caso base: string vacía if (text == EMPTY_STRING) { return; } // cuenta la frecuencia de aparición de cada personaje // y almacenarlo en un mapa unordered_map<char, int> freq; for (char ch: text) { freq[ch]++; } // Crear una cola de prioridad para almacenar nodos en vivo del árbol de Huffman priority_queue<Node*, vector<Node*>, comp> pq; // Crea un nodo hoja para cada carácter y añádelo // a la cola de prioridad. for (auto pair: freq) { pq.push(getNode(pair.first, pair.second, nullptr, nullptr)); } // hacer hasta que haya más de un nodo en la queue while (pq.size() != 1) { // Elimina los dos nodos de mayor prioridad // (la frecuencia más baja) de la queue Node* left = pq.top(); pq.pop(); Node* right = pq.top(); pq.pop(); // crea un nuevo nodo interno con estos dos nodos como hijos y // con una frecuencia igual a la suma de las frecuencias de los dos nodos. // Agregar el nuevo nodo a la cola de prioridad. int sum = left->freq + right->freq; pq.push(getNode('\0', sum, left, right)); } // `root` almacena el puntero a la raíz de Huffman Tree Node* root = pq.top(); // Atraviesa el árbol Huffman y almacena códigos Huffman // en un mapa. Además imprímelos unordered_map<char, string> huffmanCode; encode(root, EMPTY_STRING, huffmanCode); cout << "Huffman Codes are:\n" << endl; for (auto pair: huffmanCode) { cout << pair.first << " " << pair.second << endl; } cout << "\nThe original string is:\n" << text << endl; // Imprimir string codificada string str; for (char ch: text) { str += huffmanCode[ch]; } cout << "\nThe encoded string is:\n" << str << endl; cout << "\nThe decoded string is:\n"; if (isLeaf(root)) { // Caso especial: Para entradas como a, aa, aaa, etc. while (root->freq--) { cout << root->ch; } } else { // Atraviesa el árbol Huffman de nuevo y esta vez, // decodifica la string codificada int index = -1; while (index < (int)str.size() - 1) { decode(root, index, str); } } } // Implementación del algoritmo de codificación de Huffman en C++ int main() { string text = "Huffman coding is a data compression algorithm."; buildHuffmanTree(text); return 0; } |
Resultado:
Huffman Codes are:
c 11111
h 111100
f 11101
r 11100
t 11011
p 110101
i 1100
g 0011
l 00101
a 010
o 000
d 10011
H 00100
. 111101
s 0110
m 0111
e 110100
101
n 1000
u 10010
The original string is:
Huffman coding is a data compression algorithm.
The encoded string is:
00100100101110111101011101010001011111100010011110010000011101110001101010101011001101011011010101111110000111110101111001101000110011011000001000101010001010011000111001100110111111000111111101
The decoded string is:
Huffman coding is a data compression algorithm.
Java
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
import java.util.Comparator; import java.util.HashMap; import java.util.Map; import java.util.PriorityQueue; // Un nodo de árbol class Node { Character ch; Integer freq; Node left = null, right = null; Node(Character ch, Integer freq) { this.ch = ch; this.freq = freq; } public Node(Character ch, Integer freq, Node left, Node right) { this.ch = ch; this.freq = freq; this.left = left; this.right = right; } } class Main { // Atraviesa el árbol de Huffman y almacena los códigos de Huffman en un mapa. public static void encode(Node root, String str, Map<Character, String> huffmanCode) { if (root == null) { return; } // Encontré un nodo hoja if (isLeaf(root)) { huffmanCode.put(root.ch, str.length() > 0 ? str : "1"); } encode(root.left, str + '0', huffmanCode); encode(root.right, str + '1', huffmanCode); } // Atraviesa el árbol de Huffman y decodifica la string codificada public static int decode(Node root, int index, StringBuilder sb) { if (root == null) { return index; } // Encontré un nodo hoja if (isLeaf(root)) { System.out.print(root.ch); return index; } index++; root = (sb.charAt(index) == '0') ? root.left : root.right; index = decode(root, index, sb); return index; } // Función de utilidad para verificar si Huffman Tree contiene solo un solo nodo public static boolean isLeaf(Node root) { return root.left == null && root.right == null; } // Construye Huffman Tree y decodifica el texto de entrada dado public static void buildHuffmanTree(String text) { // Caso base: string vacía if (text == null || text.length() == 0) { return; } // Contar la frecuencia de aparición de cada personaje // y almacenarlo en un mapa Map<Character, Integer> freq = new HashMap<>(); for (char c: text.toCharArray()) { freq.put(c, freq.getOrDefault(c, 0) + 1); } // crea una cola de prioridad para almacenar nodos activos del árbol de Huffman. // Observe que el elemento de mayor prioridad tiene la frecuencia más baja PriorityQueue<Node> pq; pq = new PriorityQueue<>(Comparator.comparingInt(l -> l.freq)); // crea un nodo hoja para cada carácter y lo agrega // a la cola de prioridad. for (var entry: freq.entrySet()) { pq.add(new Node(entry.getKey(), entry.getValue())); } // hacer hasta que haya más de un nodo en la queue while (pq.size() != 1) { // Elimina los dos nodos de mayor prioridad // (la frecuencia más baja) de la queue Node left = pq.poll(); Node right = pq.poll(); // crea un nuevo nodo interno con estos dos nodos como hijos // y con una frecuencia igual a la suma de ambos nodos' // frecuencias. Agregue el nuevo nodo a la cola de prioridad. int sum = left.freq + right.freq; pq.add(new Node(null, sum, left, right)); } // `root` almacena el puntero a la raíz de Huffman Tree Node root = pq.peek(); // Atraviesa el árbol de Huffman y almacena los códigos de Huffman en un mapa Map<Character, String> huffmanCode = new HashMap<>(); encode(root, "", huffmanCode); // Imprime los códigos de Huffman System.out.println("Huffman Codes are: " + huffmanCode); System.out.println("The original string is: " + text); // Imprimir string codificada StringBuilder sb = new StringBuilder(); for (char c: text.toCharArray()) { sb.append(huffmanCode.get(c)); } System.out.println("The encoded string is: " + sb); System.out.print("The decoded string is: "); if (isLeaf(root)) { // Caso especial: Para entradas como a, aa, aaa, etc. while (root.freq-- > 0) { System.out.print(root.ch); } } else { // Atraviesa el árbol Huffman de nuevo y esta vez, // decodifica la string codificada int index = -1; while (index < sb.length() - 1) { index = decode(root, index, sb); } } } // Implementación del algoritmo de codificación de Huffman en Java public static void main(String[] args) { String text = "Huffman coding is a data compression algorithm."; buildHuffmanTree(text); } } |
Resultado:
Huffman Codes are: { =100, a=010, c=0011, d=11001, e=110000, f=0000, g=0001, H=110001, h=110100, i=1111, l=101010, m=0110, n=0111, .=10100, o=1110, p=110101, r=0010, s=1011, t=11011, u=101011}
The original string is: Huffman coding is a data compression algorithm.
The encoded string is: 11000110101100000000011001001111000011111011001111101110001100111110111000101001100101011011010100001111100110110101001011000010111011111111100111100010101010000111100010111111011110100011010100
The decoded string is: Huffman coding is a data compression algorithm.
Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 |
import heapq from heapq import heappop, heappush def isLeaf(root): return root.left is None and root.right is None # A Nodo de árbol class Node: def __init__(self, ch, freq, left=None, right=None): self.ch = ch self.freq = freq self.left = left self.right = right # Anule la función `__lt__()` para hacer que la clase `Node` funcione con la cola de prioridad # tal que el elemento de mayor prioridad tiene la frecuencia más baja def __lt__(self, other): return self.freq < other.freq # Atraviesa el árbol de Huffman y almacena los códigos de Huffman en un diccionario def encode(root, s, huffman_code): if root is None: return # encontró un nodo hoja if isLeaf(root): huffman_code[root.ch] = s if len(s) > 0 else '1' encode(root.left, s + '0', huffman_code) encode(root.right, s + '1', huffman_code) # Atraviesa el árbol de Huffman y decodifica la string codificada def decode(root, index, s): if root is None: return index # encontró un nodo hoja if isLeaf(root): print(root.ch, end='') return index index = index + 1 root = root.left if s[index] == '0' else root.right return decode(root, index, s) # Construye Huffman Tree y decodifica el texto de entrada dado def buildHuffmanTree(text): # Caso base: string vacía if len(text) == 0: return # cuenta la frecuencia de aparición de cada personaje # y almacenarlo en un diccionario freq = {i: text.count(i) for i in set(text)} # Crear una cola de prioridad para almacenar nodos activos del árbol de Huffman. pq = [Node(k, v) for k, v in freq.items()] heapq.heapify(pq) # hacer hasta que haya más de un nodo en la queue while len(pq) != 1: # Eliminar los dos nodos de mayor prioridad # (la frecuencia más baja) de la queue left = heappop(pq) right = heappop(pq) # crea un nuevo nodo interno con estos dos nodos como hijos y # con una frecuencia igual a la suma de las frecuencias de los dos nodos. # Agregue el nuevo nodo a la cola de prioridad. total = left.freq + right.freq heappush(pq, Node(None, total, left, right)) # `root` almacena el puntero a la raíz de Huffman Tree root = pq[0] # atraviesa el árbol de Huffman y almacena los códigos de Huffman en un diccionario huffmanCode = {} encode(root, '', huffmanCode) # imprime los códigos Huffman print('Huffman Codes are:', huffmanCode) print('The original string is:', text) # imprime la string codificada s = '' for c in text: s += huffmanCode.get(c) print('The encoded string is:', s) print('The decoded string is:', end=' ') if isLeaf(root): # Caso especial: Para entradas como a, aa, aaa, etc. while root.freq > 0: print(root.ch, end='') root.freq = root.freq - 1 else: # atraviesa el Huffman Tree nuevamente y esta vez, # decodifica la string codificada index = -1 while index < len(s) - 1: index = decode(root, index, s) # Implementación del algoritmo de codificación # Huffman en Python if __name__ == '__main__': text = 'Huffman coding is a data compression algorithm.' buildHuffmanTree(text) |
Resultado:
Huffman Codes are: {‘l’: ‘00000’, ‘p’: ‘00001’, ‘t’: ‘0001’, ‘h’: ‘00100’, ‘e’: ‘00101’, ‘g’: ‘0011’, ‘a’: ‘010’, ‘m’: ‘0110’, ‘.’: ‘01110’, ‘r’: ‘01111’, ‘ ‘: ‘100’, ‘n’: ‘1010’, ‘s’: ‘1011’, ‘c’: ‘11000’, ‘f’: ‘11001’, ‘i’: ‘1101’, ‘o’: ‘1110’, ‘d’: ‘11110’, ‘u’: ‘111110’, ‘H’: ‘111111’}
The original string is: Huffman coding is a data compression algorithm.
The encoded string is: 11111111111011001110010110010101010011000111011110110110100011100110110111000101001111001000010101001100011100110000010111100101101110111101111010101000100000000111110011111101000100100011001110
The decoded string is: Huffman coding is a data compression algorithm.
Tenga en cuenta que el almacenamiento de la string de entrada es de 47×8 = 376 bits, pero nuestra string codificada solo ocupa 194 bits, es decir, alrededor de 48% de compresión de datos. Para que el programa sea legible, hemos utilizado la clase de string para almacenar la string codificada del programa anterior.
Dado que las estructuras de datos de cola de prioridad eficientes requieren O(log(n)) tiempo por inserción, y un árbol binario completo con n hojas tiene 2n-1 nodos, y el árbol de codificación de Huffman es un árbol binario completo, este algoritmo opera en O(n.log(n)) tiempo, donde n es el número total de caracteres.
Referencias:
https://en.wikipedia.org/wiki/Huffman_coding
https://en.wikipedia.org/wiki/Variable-length_code
Dr. Naveen Garg, IIT–D (Conferencia – 19 Compresión de datos)